Integral of 1÷(x⁵+1)

While I was meaninglessly scrolling reels of Instagram, this showed up.

Well, if that showed up on the exam, what else we gonna do?

Scenario

I immediately thought of an idea, to factorize the denominator, and make the expression

into sum of fractions with 1-degreed denominator.

For test if my scenario would actually work, I tested with $\int_{0}^{1}\frac{1}{x^2 + 1}$.

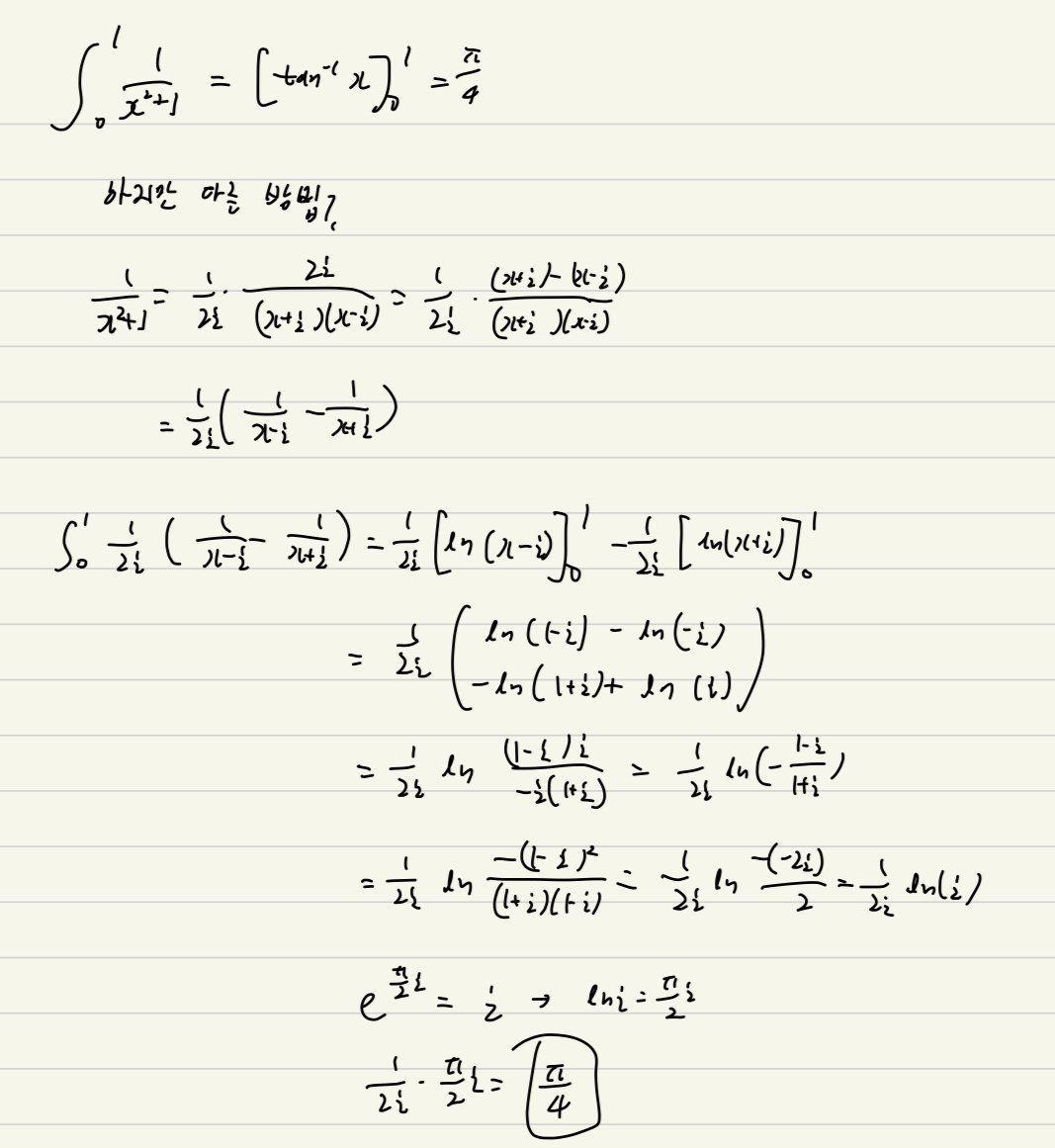
It nicely resulted as $\frac{\pi}{4}$.

1. Factorizing $x^5 + 1$

It is quite easy to factorize $x^5 + 1$ if you know well about complex field.

If we define $\alpha$ as $(e^{\pi i})^{\frac{1}{5}} = e^{\frac{\pi}{5}i}$, $\alpha$ would be a root for $x^5 + 1 = 0$.

For other roots, we can muntiply $(e^{2 \pi i})^{\frac{1}{5}} = e^{\frac{2\pi}{5}i}$ 0 ~ 4 times. Let’s call it $\beta$.

Then $x^5 + 1$ can be factorized as:

$(x - \alpha)(x - \alpha\beta)(x - \alpha\beta^2)(x - \alpha\beta^3)(x - \alpha\beta^4)$

2. Finding the coefficients for each fractions

The goal is to find constants $C_{0} \sim C_{4}$ which satisfies:

$\frac{1}{x^5 + 1} = \frac{C_{0}}{x - \alpha} + \frac{C_{1}}{x - \alpha\beta} + \frac{C_{2}}{x - \alpha\beta^2} + \frac{C_{3}}{x - \alpha\beta^3} + \frac{C_{4}}{x - \alpha\beta^4}$

Five is too many, let’s just see how it works with 3, and make someone else calculate the rest.

$\frac{1}{(x - \alpha)(x - \alpha\beta)(x - \alpha\beta^2)} = \frac{C_{0}}{x - \alpha} + \frac{C_{1}}{x - \alpha\beta} + \frac{C_{2}}{x - \alpha\beta^2}$

We first can express first two like this.

$\frac{1}{(x - \alpha)(x - \alpha\beta)} = \frac{1}{\alpha - \alpha\beta}(\frac{1}{x - \alpha} - \frac{1}{x - \alpha\beta})$

Then, we multiply one more, and repeat the same step.

$\frac{1}{(x - \alpha)(x - \alpha\beta)(x - \alpha\beta^2)} = \frac{1}{\alpha - \alpha\beta}(\frac{1}{(x - \alpha)(x - \alpha\beta^2)} - \frac{1}{(x - \alpha\beta)(x - \alpha\beta^2)})$

It is stupid to do this by hand, and I don’t know a smart way to ask Wolfram|Alpha about this.

So let’s use god SageMath with R.<a, b> = PolynomialRing(QQ, 'a, b').

Also it’s cheating to use Wolfram|Alpha during exam.

(SageMath isn’t because it can be ran offline.)

(I am not accepting any counterarguments.)

coef.sage

R.<a, b> = PolynomialRing(QQ, 'a, b')

coefs = [1, 0, 0, 0, 0]

for i in range(1, 5):
    new_coefs = [0] * 5

    for j in range(i):
        # 1 / (x - ab^j)(x - ab^i)
        # i > j
        
        # = 1 / (ab^j - ab^i) * 1 / (x - ab^j)
        # + 1 / (ab^i - ab^j) * 1 / (x - ab^i)

        new_coefs[j] += 1 / (a * b^j - a * b^i) * coefs[j]
        new_coefs[i] += 1 / (a * b^i - a * b^j) * coefs[j]

    coefs = new_coefs

print(coefs)

[1/(a^4*b^10 - a^4*b^9 - a^4*b^8 + 2*a^4*b^5 - a^4*b^2 - a^4*b + a^4), 1/(-a^4*b^10 + 2*a^4*b^9 - a^4*b^7 - a^4*b^6 + 2*a^4*b^4 - a^4*b^3), (-1)/(-a^4*b^11 + 2*a^4*b^10 + a^4*b^9 - 4*a^4*b^8 + a^4*b^7 + 2*a^4*b^6 - a^4*b^5), 1/(-a^4*b^13 + 2*a^4*b^12 - a^4*b^10 - a^4*b^9 + 2*a^4*b^7 - a^4*b^6), (-1)/(-a^4*b^16 + a^4*b^15 + a^4*b^14 - 2*a^4*b^11 + a^4*b^8 + a^4*b^7 - a^4*b^6)]

This list represents $C_{0} \sim C_{4}$ I mentioned before.

It looks dirty. But why don’t we add a simple trick?

b = a^2

coef.sage

R.<a, b> = PolynomialRing(QQ, 'a, b')
b = a^2

coefs = [1, 0, 0, 0, 0]

for i in range(1, 5):
    new_coefs = [0] * 5

    for j in range(i):
        # 1 / (x - ab^j)(x - ab^i)
        # i > j
        
        # = 1 / (ab^j - ab^i) * 1 / (x - ab^j)
        # + 1 / (ab^i - ab^j) * 1 / (x - ab^i)

        new_coefs[j] += 1 / (a * b^j - a * b^i) * coefs[j]
        new_coefs[i] += 1 / (a * b^i - a * b^j) * coefs[j]

    coefs = new_coefs

print(coefs)

[1/(a^24 - a^22 - a^20 + 2*a^14 - a^8 - a^6 + a^4), 1/(-a^24 + 2*a^22 - a^18 - a^16 + 2*a^12 - a^10), (-1)/(-a^26 + 2*a^24 + a^22 - 4*a^20 + a^18 + 2*a^16 - a^14), 1/(-a^30 + 2*a^28 - a^24 - a^22 + 2*a^18 - a^16), (-1)/(-a^36 + a^34 + a^32 - 2*a^26 + a^20 + a^18 - a^16)]

Much better right?

We can add something like a^5 = -1 too, but let’s do it when final calculating part comes.

3. Calculating the Integral

It is well known to get the integral of $\frac{1}{x + k}$, it is $\ln(x + k)$.

So we can conclude that the integral of $x^5 + 1$ is:

$C_{0}\ln(x - \alpha) + C_{1}\ln(x - \alpha\beta) + C_{2}\ln(x - \alpha\beta^2) + C_{3}\ln(x - \alpha\beta^3) + C_{4}\ln(x - \alpha\beta^4)$

According to Wolfram|Alpha, it can be way more modified, but who cares.

Now let’s check if we got it correct.

I implemented a script which calculates integral from $A$ to $B$.

solve.sage

a = e ^ (pi * i / 5)
b = a^2

coefs = [1/(a^24 - a^22 - a^20 + 2*a^14 - a^8 - a^6 + a^4), 1/(-a^24 + 2*a^22 - a^18 - a^16 + 2*a^12 - a^10), (-1)/(-a^26 + 2*a^24 + a^22 - 4*a^20 + a^18 + 2*a^16 - a^14), 1/(-a^30 + 2*a^28 - a^24 - a^22 + 2*a^18 - a^16), (-1)/(-a^36 + a^34 + a^32 - 2*a^26 + a^20 + a^18 - a^16)]

A, B = 0, 1

ans = 0

for i in range(5):
    ans += coefs[i] * (ln(B - a * b^i) - ln(A - a * b^i))

print(ans)

And let’s compare the result with the answer.

-4722366482869645213696*(log(-1/262144*(sqrt(5) + I*sqrt(-2*sqrt(5) + 10) + 1)^9) - log(-1/262144*(sqrt(5) + I*sqrt(-2*sqrt(5) + 10) + 1)^9 + 1))/((sqrt(5) + I*sqrt(-2*sqrt(5) + 10) + 1)^36 - 16*(sqrt(5) + I*sqrt(-2*sqrt(5) + 10) + 1)^34 - 256*(sqrt(5) + I*sqrt(-2*sqrt(5) + 10) + 1)^32 + 2097152*(sqrt(5) + I*sqrt(-2*sqrt(5) + 10) + 1)^26 - 4294967296*(sqrt(5) + I*sqrt(-2*sqrt(5) + 10) + 1)^20 - 68719476736*(sqrt(5) + I*sqrt(-2*sqrt(5) + 10) + 1)^18 + 1099511627776*(sqrt(5) + I*sqrt(-2*sqrt(5) + 10) + 1)^16) + 1152921504606846976*(log(-1/16384*(sqrt(5) + I*sqrt(-2*sqrt(5) + 10) + 1)^7) - log(-1/16384*(sqrt(5) + I*sqrt(-2*sqrt(5) + 10) + 1)^7 + 1))/((sqrt(5) + I*sqrt(-2*sqrt(5) + 10) + 1)^30 - 32*(sqrt(5) + I*sqrt(-2*sqrt(5) + 10) + 1)^28 + 4096*(sqrt(5) + I*sqrt(-2*sqrt(5) + 10) + 1)^24 + 65536*(sqrt(5) + I*sqrt(-2*sqrt(5) + 10) + 1)^22 - 33554432*(sqrt(5) + I*sqrt(-2*sqrt(5) + 10) + 1)^18 + 268435456*(sqrt(5) + I*sqrt(-2*sqrt(5) + 10) + 1)^16) - 4503599627370496*(log(-1/1024*(sqrt(5) + I*sqrt(-2*sqrt(5) + 10) + 1)^5) - log(-1/1024*(sqrt(5) + I*sqrt(-2*sqrt(5) + 10) + 1)^5 + 1))/((sqrt(5) + I*sqrt(-2*sqrt(5) + 10) + 1)^26 - 32*(sqrt(5) + I*sqrt(-2*sqrt(5) + 10) + 1)^24 - 256*(sqrt(5) + I*sqrt(-2*sqrt(5) + 10) + 1)^22 + 16384*(sqrt(5) + I*sqrt(-2*sqrt(5) + 10) + 1)^20 - 65536*(sqrt(5) + I*sqrt(-2*sqrt(5) + 10) + 1)^18 - 2097152*(sqrt(5) + I*sqrt(-2*sqrt(5) + 10) + 1)^16 + 16777216*(sqrt(5) + I*sqrt(-2*sqrt(5) + 10) + 1)^14) + 281474976710656*(log(-1/64*(sqrt(5) + I*sqrt(-2*sqrt(5) + 10) + 1)^3) - log(-1/64*(sqrt(5) + I*sqrt(-2*sqrt(5) + 10) + 1)^3 + 1))/((sqrt(5) + I*sqrt(-2*sqrt(5) + 10) + 1)^24 - 32*(sqrt(5) + I*sqrt(-2*sqrt(5) + 10) + 1)^22 + 4096*(sqrt(5) + I*sqrt(-2*sqrt(5) + 10) + 1)^18 + 65536*(sqrt(5) + I*sqrt(-2*sqrt(5) + 10) + 1)^16 - 33554432*(sqrt(5) + I*sqrt(-2*sqrt(5) + 10) + 1)^12 + 268435456*(sqrt(5) + I*sqrt(-2*sqrt(5) + 10) + 1)^10) + 281474976710656*(log(-1/4*sqrt(5) - 1/4*I*sqrt(-2*sqrt(5) + 10) + 3/4) - log(-1/4*sqrt(5) - 1/4*I*sqrt(-2*sqrt(5) + 10) - 1/4))/((sqrt(5) + I*sqrt(-2*sqrt(5) + 10) + 1)^24 - 16*(sqrt(5) + I*sqrt(-2*sqrt(5) + 10) + 1)^22 - 256*(sqrt(5) + I*sqrt(-2*sqrt(5) + 10) + 1)^20 + 2097152*(sqrt(5) + I*sqrt(-2*sqrt(5) + 10) + 1)^14 - 4294967296*(sqrt(5) + I*sqrt(-2*sqrt(5) + 10) + 1)^8 - 68719476736*(sqrt(5) + I*sqrt(-2*sqrt(5) + 10) + 1)^6 + 1099511627776*(sqrt(5) + I*sqrt(-2*sqrt(5) + 10) + 1)^4)

Uh oh, this doesn’t look so nice.

The reason for this is, sage is too careful so it doesn’t lose data for my inputs, and can’t proceed calculating.

It’s okay sage, you can lose some data hehe.

Let’s add RealField.

solve.sage

R = RealField(100)

a = R(e) ^ (R(pi) * i / R(5))
b = a^2

coefs = [1/(a^24 - a^22 - a^20 + 2*a^14 - a^8 - a^6 + a^4), 1/(-a^24 + 2*a^22 - a^18 - a^16 + 2*a^12 - a^10), (-1)/(-a^26 + 2*a^24 + a^22 - 4*a^20 + a^18 + 2*a^16 - a^14), 1/(-a^30 + 2*a^28 - a^24 - a^22 + 2*a^18 - a^16), (-1)/(-a^36 + a^34 + a^32 - 2*a^26 + a^20 + a^18 - a^16)]

A, B = 0, 1

ans = 0

for i in range(5):
    ans += coefs[i] * (ln(B - a * b^i) - ln(A - a * b^i))

print(ans)

0.88831357265178863804075522702 + 2.7610131682735413189410499785e-30*I

Now!!! That’s more like it.

Do you think I’ll get high score for the exam?

If I get F for cheating using sage, professor and I am gonna have some deep talk.