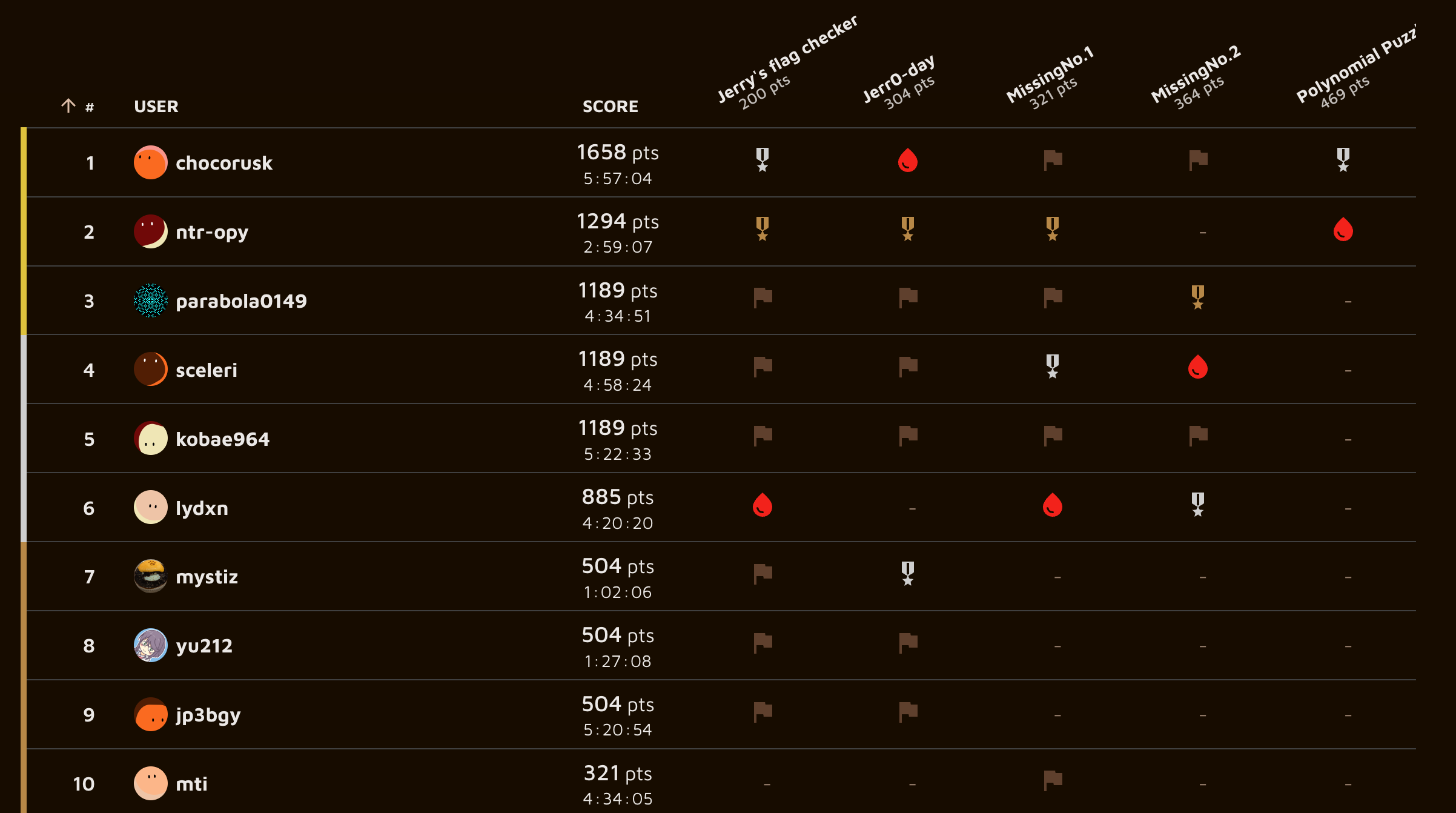
Alpacahack Round 13 (Crypto)
I authored all 5 challenges for Alpacahack Round 13, which was held this Sunday. Thanks to all the people who played it, and I hope they had fun. Congrats to Chocorusk for winning this round!
This post will include a very brief explanation of the solutions, and some additional fun related to them. You can find all solve code in my-ctf-challenges. Note that the distfiles may be slightly different between what’s in the repo and the actual files. Some additional editing and trimming were done by keymoon.
Jerry’s flag checker (21 solves)
Jerry will verify your flag for you!
from Crypto.Util.number import *
import os
flag = bytes_to_long(os.environ.get("FLAG", "fakeflag").encode())
while True:
try:
if long_to_bytes(int(input("Guess the flag in integer: ")) - flag).decode():
print("Wrong flag. :P")
else:
print("Yay, you found the flag! :3")
except:
print("Weird... :/")
It can be seen that the .decode() and the try-except are meant to be some kind of oracle, and give the user some information for a solve. The only key part for this simple challenge is to find one initial input that satisfies the condition, then it can be easily found by bruting byte-by-byte.
Assuming all flag bytes are ASCII, they must be in the range of [32, 127). Thus, first guess the number of flag length, then sending bytes_to_long(b"\x7f\x7f\x7f\x7f...") can make it print "Wrong flag. :P" instead of "Weird... :/". Note that this method even allows you not to guess the flag’s length, since you can just put a long string like 100 bytes, and it’ll still succeed to decode.
Alpaca{ASCII_oracle_attack!!}
I remember asking my friend JoshL, one of the sexiest reversers, for a testsolve cuz we were on a long trip together then(Of course, I told him he can’t participate). Josh suggested the solution above, which is even cleaner than my intended solution using "\x80" in my opinion.
Something like the following can be done too, since it gives the same oracle, but requires multiple connections. This makes it less obvious for a solution, but it’s a warm-up challenge anyway, and also prevents excessive connections. I chose to use a while loop.
from Crypto.Util.number import *
import os
flag = bytes_to_long(os.environ.get("FLAG", "fakeflag").encode())
if long_to_bytes(int(input("Guess the flag in integer: ")) - flag).decode():
print("Wrong flag. :P")
else:
print("Yay, you found the flag! :3")
Jerr0-day (8 solves)
Jerry thinks he discovered a 0-day!
from py_ecc import bn128
from ast import literal_eval
def recv_G1():
return tuple(bn128.FQ(val) for val in literal_eval(input("Input G1: ")))
def recv_G2():
return tuple(bn128.FQ2(val) for val in literal_eval(input("Input G2: ")))
A, B = recv_G1(), recv_G1()
C = recv_G2()
if (
bn128.pairing(C, A) * bn128.pairing(C, B)
==
bn128.pairing(C, bn128.add(A, B))
):
print("Looks like it's safe!")
else:
import os
print(os.environ.get("FLAG", "fakeflag"))
This seems impossible at first glance if you know about pairings. I wish wonder if someone even tried to use the zero point or something, cuz that point always causes issues, but shouldn’t work.
If you’re familiar with pairing-friendly curves, you should know the curve for G2 affine is actually not the curve itself; it’s always a subgroup of a curve. This means if there’s only an on-curve check and no subgroup check, invalid G2 points that don’t follow pairing’s property can be used in the py-ecc package.
Turns out there’s no subgroup check. py_ecc:
# Pairing computation
def pairing(Q: Point2D[FQ2], P: Point2D[FQ]) -> FQ12:
if not is_on_curve(Q, b2):
raise ValueError("Invalid input - point Q is not on the correct curve")
if not is_on_curve(P, b):
raise ValueError("Invalid input - point P is not on the correct curves")
return miller_loop(twist(Q), cast_point_to_fq12(P))
# Check that a point is on the curve defined by y**2 == x**3 + b
def is_on_curve(pt: Point2D[Field], b: Field) -> bool:
if is_inf(pt) or pt is None:
return True
x, y = pt
return y**2 - x**3 == b
Simply sending a random point in the G2 curve messes up the pairing result and solves the challenge.
from pwn import *
io = remote("localhost", 9997)
q = 21888242871839275222246405745257275088696311157297823662689037894645226208583
r = 21888242871839275222246405745257275088548364400416034343698204186575808495617
F = GF(q)
F2.<u> = GF(q^2, modulus=x^2 + 1)
E = EllipticCurve(F, [0, 3])
E2 = EllipticCurve(F2, [0, 3 / (u + 9)])
A, B = E.random_element(), E.random_element()
assert A * r == B * r == E(0)
C = E2.random_element()
assert C * r != E2(0)
io.sendlineafter(b"Input G1: ", str(A.xy()).encode())
io.sendlineafter(b"Input G1: ", str(B.xy()).encode())
io.sendlineafter(b"Input G2: ", str(tuple(tuple(val) for val in C.xy())).encode())
io.interactive()
Alpaca{Not-a-0day-https://github.com/Consensys/gnark-crypto/blob/master/ecc/bn254/g2.go#L208-L226}
Out of context, I love the name Jerr0-day cuz 0 is leetcoded o, so that it has substring 0-day inside, and Jerroday is pronounced very similar to zeroday. And most importantly I am Jerry.
MissingNo.1 (7 solves)
I think the original challenge from Neobeo is too easy… This is a revenge challenge of MissingNo. from OICC 2025.
FLAG = os.environ.get("FLAG", "Alpaca{********************************************}").encode()
F = GF(0xdead1337cec2a21ad8d01f0ddabce77f57568d649495236d18df76b5037444b1)
A = random_matrix(F, len(FLAG))[:,:-2]
b = A * random_vector(F, A.ncols()) + vector(F, FLAG) * F.random_element()
print(dumps((A, b)).hex())
The source code looks completely identical except for the [:,:-2], which if you understand the original challenge’s solution, is not really solvable with the same method. However, a server is given and you can gather multiple information by connecting more than once.
Efficiently, with two connections, it’s possible to get the same amount of information from the original challenge and solve via LLL/BKZ. But with even more, LLL is not even needed. Check out solve.sage with 2 connections, and solve_9.sage with 9 connections and no LLL. But I didn’t block that solution, since this challenge is also supposed to be a level 2. But instead, I complained in the flag.
Alpaca{Sad_if_you_used_more_than_2_connections__>:(}
I am aware that the real challenge code looked a bit more complex due to the fix, while I wanted the difference from the original challenge to be as minimal as possible… Hope it didn’t make players try to spot bugs in another place, e.g., utils.py.
MissingNo.2 (5 solves)
This time the fix must have made it safe enough! This is a revenge challenge of MissingNo. from OICC 2025.
FLAG = os.environ.get("FLAG", "Alpaca{********************************************}").encode()
pad = os.urandom(len(FLAG))
FLAG = [a ^^ b for a, b in zip(FLAG, pad)]
q = int(input("Missing order: "), 16)
assert not is_prime(q) and q.bit_length() == 256
F = GF(q)
A = random_matrix(F, len(FLAG))[:,:-2]
b = A * random_vector(F, A.ncols()) + vector(F, FLAG) * F.random_element()
print(dumps((A, b, pad)).hex())
Seems pretty much the same, but this time you can set the GF order to a 256-bit integer you like, and the flag is XORed with a known OTP every connection. The XOR blocks the solution for MissingNo.1.
If we call A’s two left_kernel vector v1, v2, then:
v1 * b = (v1 * FLAG) * F_random_element(v1 * b) * (v2 * FLAG) = (v2 * FLAG) * (v1 * FLAG) * F_random_element
v2 * b = (v2 * FLAG) * F_random_element(v2 * b) * (v1 * FLAG) = (v1 * FLAG) * (v2 * FLAG) * F_random_element
Thus:
(v1 * b) * (v2 * FLAG) - (v2 * b) * (v1 * FLAG) = 0((v1 * b) * v2 - (v2 * b) * v1) * FLAG = 0
Ok, so we know a nullspace of FLAG, whose length is 52 (This is not any different from MissingNo. or MissingNo.1, but just re-explaining), and the FLAG is only composed of 52 integer terms of the field, no terms multiplied by the Field’s generator. This means if the field’s power is 52 or more, you can just solve the linear equations.
Let’s see the order $37^{49}$ I used for my solution. Since we know the flag format Alpaca{}, there are only 44 unknowns, and with 49 equations, the system is solvable. However, we can only know the FLAG modulus 37. No problem, that’s where multiple connections & XOR pads help. Gathering 2 ~ 4 information by multiple connections will be enough for 44 unknown values to have a single possible candidate.
Check out solve.sage.
Alpaca{Oh_I_forgor_GF_allows_these_weird_values_:'(}
Polynomial Puzzle (2 solves)
You know you have to kill Daki and Gyutaro at the same to beat them right? This is a revenge challenge of Polynomial Game from LakeCTF ‘24-‘25 Finals.
K = GF(random_prime(2 ^ 35))
R = K["x"]
d = 20
f = R.random_element(degree=d)
print("Welcome to the Polynomial Puzzle!")
print(f"f(x) is a univariate degree {d} polynomial with coefficients in K = {K}")
for _ in range(d + 3):
x = next_prime(K.random_element())
mixed = [K.random_element() for _ in "apch"]
mixed[1] = f(x) - mixed[0]
shuffle(mixed)
print(f"f({x}) is sum of some two values of {mixed}")
guess = int(input("What is f(42)?\n> "))
if guess == f(42):
print(f"You won! The flag is {os.environ.get("FLAG", "fakeflag")}")
else:
print("You lost :(")
I first failed to solve this during LakeCTF finals this year (LOL), but my GOAT genni cooked it with LLL, and I thought it was quite clever, and made this revenge challenge.
SADLY, the winner Chocorusk used MITM, which was unintended, and also my skill issue.


My life…
But still, I’m happy to see the following:
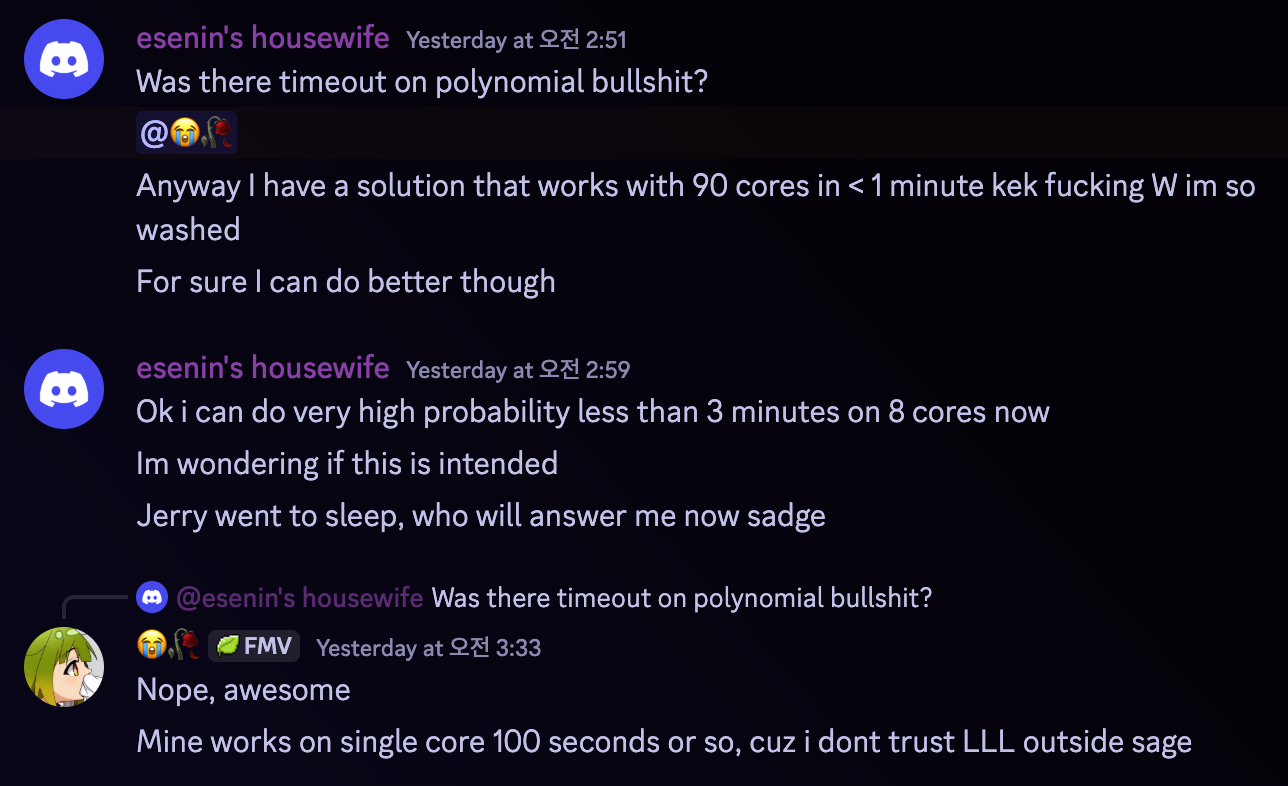
Neobeo, the old man suspiciously knows ntr-opy very well…
The LLL.
I won’t write the full solution here since you have solve.sage, but the key idea and some details.
There are 21 unknown coefficients, and 23 information, so it gives an extra 35 * 2 = 70 bits. However, it loses some information since $_4C_2 = 6$ possibilities exist for each pair. $6^{23}$ is 60 bit, so it is theoretically possible to solve.
Let’s try the strategy that constraints every 4 values to be 0 or 1.
The reduced lattice will give the 5th value of the vector sum of some values in the pool of 4. Unfortunately, there are 16 possibilities if you use a lattice in this form. $16^{23}$ is 92 bits, which is undoable with extra info of 70 bits.
How can we cleverly use the $_4C_2$ fact? Only two out of 4 are 1, and the other 2 are 0, which means the sum of those 4 is always 2.
In this form of lattice, we can fully force the constraint of $_4C_2$, and make the 6th value of the reduced vector only the sum of two values in $v_0, v_1, v_2, v_3$.
But this kinda makes the matrix larger, and I chose to only variable-ize 3 of them instead of 4, and make $a_3 = 2 - (a_0 + a_1 + a_2)$, and force $a_0, a_1, a_2$ to be in [0, 1]. This reduces the number of variables from 4 to 3, however $2^3 = 8$ possibilities instead of 6. $8^{23}$ is 69 bits, so it is in a very tight range.
EDIT AFTER POSTING) But this kinda makes the matrix larger This line is somehow true and somehow may not matter much, can you find a better solution via lattice than the current solve code?
Some extra notes to deal with the tight range:
- My solution uses two LLL, the first one is done very quickly and doesn’t even need that much precision.
- The second LLL is important, I used SageMath’s BKZ(block_size=40) for a 70x70 size matrix. Note that $70 = 23 * 3 + 1$.
- I tried to make $p$ as large as possible to get as much information as possible, so it disconnects directly until $p > 0.9 * 2^{35}$.
Alpaca{Sorry_for_BKZ_requiring_params_but_I_had_to_block_the_naive_solution_>:)}
Note that the naive solution meant LLL via setting the constraints for all 4 * 23 values to be in [0, 1]. The naive solution is NOT the MITM @sceleri…
The MITM.
So, at least 3 people succeeded in solving this via MITM. Let’s see how it can be done.
There are $6^{23}$ possibilities, based on the possible selections, which is 60 bits. It’s definitely not brute-able, but it is in MITM-able range. But seems MITM is not so trivial in this case :thinking:…
Lagrange to the rescue
We have 23 $x$ values, and $f(x)$ is one of 6 known values. Via Lagrange interpolation, we can find some polynomial $f_i(x_i) = 1$ and $f_i(x_j) = 0 (j \neq i)$, and $f_j$ is a polynomial of 23 coefficients, thus degree 22.
And then we can write $f(x) = f_0(x)a_0 + f_1(x)a_1 + \cdots + f_{22}(x)a_{22}$, where $a_i$ are the values we selected from $_4C_2 = 6$ possible pool. But we do know $f(x)$ is degree 20, right? So the coefficient of $x^{21}, x^{22}$ must be 0, and now this is in a MITM-able condition.
This Lagrange interpolation can be used as a way to solve via LLL. Not too much different tho.
Unintends are always sad, but hey, I think this is quite a fun solution as well, and it didn’t make the challenge too easy anyway. But not gonna lie, I’m curious about the number of solves if MITM wasn’t doable.