2023 pbctf
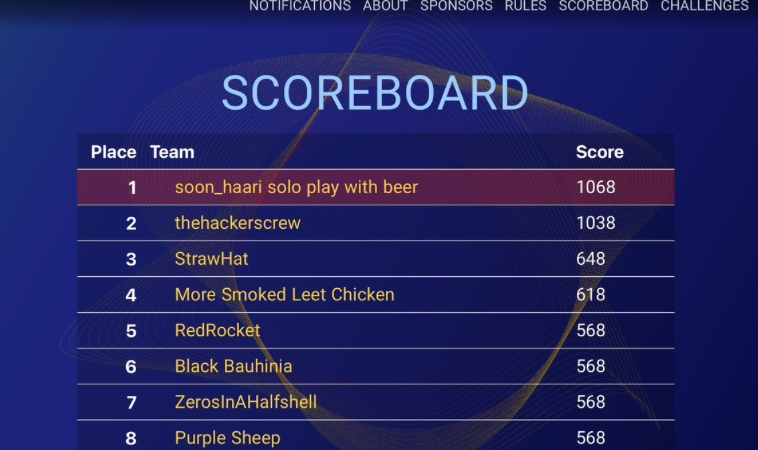
I decided to run pbctf alone this time, as team ‘soon_haari solo play with beer’.
Ended up with 26th position. If I have solved Blocky 4, which is about a famous attack for ciphers with low rounds(and considered easier than ECC2 which I have solved), maybe I have ended 21st, or even 14th if I solved the harder version of it, but it’s all fun and games.
Being top 1 for an hour, and having a first blood felt nice, hehe.
Blocky - 0 (143 solves)
All this GF(3) idea for the new AES was very interesting.
Although none of the challenges use the vulnerabilities inside that I think.
task.py
#!/usr/bin/env python3
import hashlib
import os
import signal
from Cipher import BlockCipher
from GF import GF
def handler(_signum, _frame):
print("Time out!")
exit(0)
def get_random_block():
block = b''
while len(block) < 9:
b = os.urandom(1)
if b[0] < 243:
block += b
return block
def get_mac(pt):
mac = hashlib.sha256(pt).digest()[:9]
return bytes([x % 243 for x in mac])
def pad(pt):
mac = get_mac(pt)
v = 9 - len(pt) % 9
return pt + bytes([v] * v) + mac
def unpad(pt):
if len(pt) < 18 or len(pt) % 9 != 0:
return
pt, mac = pt[:-9], pt[-9:]
if not (1 <= pt[-1] <= 9):
return
pt = pt[:-pt[-1]]
if mac == get_mac(pt):
return pt
def add(a, b):
return bytes([(GF(x) + GF(y)).to_int() for x, y in zip(a, b)])
def sub(a, b):
return bytes([(GF(x) - GF(y)).to_int() for x, y in zip(a, b)])
def main():
signal.signal(signal.SIGALRM, handler)
signal.alarm(60)
key = get_random_block()
cipher = BlockCipher(key, 20)
while True:
inp = input("> ")
if inp == 'E':
inp = input("Input (in hex): ")
inp = bytes.fromhex(inp)
assert len(inp) < 90
assert all(b < 243 for b in inp)
if inp == 'gimmeflag':
print("Result: None")
continue
pt = pad(inp)
iv = get_random_block()
enc = iv
for i in range(0, len(pt), 9):
t = add(pt[i:i+9], iv)
iv = cipher.encrypt(t)
enc += iv
print(f"Result: {enc.hex()}")
elif inp == 'D':
inp = input("Input (in hex): ")
inp = bytes.fromhex(inp)
assert len(inp) < 108
assert all(b < 243 for b in inp)
iv, ct = inp[:9], inp[9:]
dec = b''
for i in range(0, len(ct), 9):
t = cipher.decrypt(ct[i:i+9])
dec += sub(t, iv)
iv = ct[i:i+9]
pt = unpad(dec)
if pt == b'gimmeflag':
with open('flag', 'r') as f:
flag = f.read()
print(flag)
exit(0)
elif pt:
print(f"Result: {pt.hex()}")
else:
print("Result: None")
if __name__ == "__main__":
main()
It filters ‘gimmeflag’ in the encryption function, but it doesn’t filter additional blocks in the end.
So it worked when I just encrypted the padded message itself, cuz it is ‘gimmeflag{blahblahblah}. Not much of a hard challenge.
ex.py
from pwn import *
from Crypto.Util.number import *
import hashlib
def get_mac(pt):
mac = hashlib.sha256(pt).digest()[:9]
return bytes([x % 243 for x in mac])
def pad(pt):
mac = get_mac(pt)
v = 9 - len(pt) % 9
return pt + bytes([v] * v) + mac
def unpad(pt):
if len(pt) < 18 or len(pt) % 9 != 0:
return
pt, mac = pt[:-9], pt[-9:]
if not (1 <= pt[-1] <= 9):
return
pt = pt[:-pt[-1]]
if mac == get_mac(pt):
return pt
goal = pad(b"gimmeflag")
assert unpad(goal) == b"gimmeflag"
# print(len(goal))
io = remote("blocky-0.chal.perfect.blue", 1337)
io.sendline("E")
io.sendline(bytes.hex(goal))
io.recvuntil("Result: ")
enc = bytes.fromhex(io.recvline().decode()[:-1])
enc = enc[:36]
io.sendline("D")
io.sendline(bytes.hex(enc))
io.interactive()
Also, I heard that just encrypting ‘gimmeflag’ works because b”gimmeflag” isn’t same to “gimmeflag”….
My ECC Service (32 solves)
challenge.py
from Crypto.Util.number import inverse
from hashlib import sha256
import os
import signal
class NonceGenerator:
def __init__(self):
self.state = os.urandom(10)
self.db = {}
def gen(self):
self.state = sha256(self.state + b'wow').digest()[:10]
key = sha256(self.state).digest()[:8]
self.db[key] = self.state
return int.from_bytes(self.state, 'big'), key
def get(self, key: str):
if key not in self.db:
print("Wrong key :(")
exit(0)
return int.from_bytes(self.db[key], 'big')
class ECPoint:
def __init__(self, point, mod):
self.x = point[0]
self.y = point[1]
self.mod = mod
def inf(self):
return ECPoint((0, 0), self.mod)
def _is_inf(self):
return self.x == 0 and self.y == 0
def __eq__(self, other):
assert self.mod == other.mod
return self.x == other.x and self.y == other.y
def __add__(self, other):
assert self.mod == other.mod
P, Q = self, other
if P._is_inf() and Q._is_inf():
return self.inf()
elif P._is_inf():
return Q
elif Q._is_inf():
return P
if P == Q:
lam = (3 * P.x**2 - 3) * inverse(2 * P.y, self.mod) % self.mod
elif P.x == Q.x:
return self.inf()
else:
lam = (Q.y - P.y) * inverse(Q.x - P.x, self.mod) % self.mod
x = (lam**2 - P.x - Q.x) % self.mod
y = (lam * (P.x - x) - P.y) % self.mod
return ECPoint((x, y), self.mod)
def __rmul__(self, other: int):
base, ret = self, self.inf()
while other > 0:
if other & 1:
ret = ret + base
other >>= 1
base = base + base
return ret
class MyECCService:
BASE_POINT = (2, 3)
MODS = [
942340315817634793955564145941,
743407728032531787171577862237,
738544131228408810877899501401,
1259364878519558726929217176601,
1008010020840510185943345843979,
1091751292145929362278703826843,
793740294757729426365912710779,
1150777367270126864511515229247,
763179896322263629934390422709,
636578605918784948191113787037,
1026431693628541431558922383259,
1017462942498845298161486906117,
734931478529974629373494426499,
934230128883556339260430101091,
960517171253207745834255748181,
746815232752302425332893938923,
]
def __init__(self):
self.nonce_gen = NonceGenerator()
def get_x(self, nonce: int) -> bytes:
ret = b""
for mod in self.MODS:
p = ECPoint(self.BASE_POINT, mod)
x = (nonce * p).x
ret += x.to_bytes(13, "big")
return ret
def gen(self) -> bytes:
nonce, key = self.nonce_gen.gen()
x = self.get_x(nonce)
return b"\x02\x03" + key + x
def verify(self, inp: bytes) -> bool:
assert len(inp) == 218
nonce = self.nonce_gen.get(inp[2:10])
self.BASE_POINT = (inp[0], inp[1])
x = self.get_x(nonce)
return inp[10:] == x
def handler(_signum, _frame):
print("Time out!")
exit(0)
def main():
signal.signal(signal.SIGALRM, handler)
signal.alarm(300)
service = MyECCService()
for _ in range(100):
service.gen()
while True:
inp = input("> ")
if inp == "G":
payload = service.gen()
print(f"Payload: {payload.hex()}")
elif inp == "V":
payload = bytes.fromhex(input("Payload: "))
result = service.verify(payload)
print(f"Result: {result}")
elif inp == "P":
payload = bytes.fromhex(input("Payload: "))
answer = service.gen()
if payload == answer:
with open("flag.txt", "r") as f:
print(f.read())
else:
print("Wrong :(")
exit(0)
if __name__ == "__main__":
main()
We have to find the nonce which is multiplied to the base point for different curves.
We just have to break one of the 16 curves because the same nonce is used for all 16.
Factoring the orders of 16 curves gives is the result that 13th curve is factored well with small primes to use pohlig-hellman.
ex.sage
MODS = [
942340315817634793955564145941,
743407728032531787171577862237,
738544131228408810877899501401,
1259364878519558726929217176601,
1008010020840510185943345843979,
1091751292145929362278703826843,
793740294757729426365912710779,
1150777367270126864511515229247,
763179896322263629934390422709,
636578605918784948191113787037,
1026431693628541431558922383259,
1017462942498845298161486906117,
734931478529974629373494426499,
934230128883556339260430101091,
960517171253207745834255748181,
746815232752302425332893938923,
]
from pwn import *
from Crypto.Util.number import *
from hashlib import sha256
io = remote("my-ecc-service.chal.perfect.blue", 1337)
io.sendlineafter("> ", "G")
io.recvuntil("Payload: ")
recv_dat = bytes.fromhex(io.recvline().decode()[:-1])
assert len(recv_dat) == 218
original_key = recv_dat[2:10]
recv_dat = recv_dat[10:]
x_ = []
for i in range(16):
x_.append(int.from_bytes(recv_dat[:13], "big"))
recv_dat = recv_dat[13:]
E = EllipticCurve(GF(MODS[12]), [-3, 7])
G = E(2, 3)
print(G * 2)
P = E.lift_x(Integer(x_[12]))
n = G.order()
fac = list(factor(n))
print(fac)
moduli = []
remainder = []
for i, j in fac:
mod = i**j
_g_ = G * ZZ(n / mod)
_q_ = P * ZZ(n / mod)
dl = discrete_log(_q_, _g_, operation = "+")
moduli.append(mod)
remainder.append(dl)
print(dl, mod)
nonce = long_to_bytes(crt(remainder,moduli))
if len(nonce) != 10:
nonce = long_to_bytes(MODS[12] - bytes_to_long(nonce))
state = sha256(nonce + b'wow').digest()[:10]
key = sha256(state).digest()[:8]
io.sendlineafter("> ", "V")
io.sendlineafter("Payload: ", "0000" + bytes.hex(original_key) + "00" * 13 * 16)
io.sendlineafter("> ", "P")
io.sendlineafter("Payload: ", "0203" + bytes.hex(key) + "00" * 13 * 16)
io.interactive()
My ECC Service 2 (11 solves)
The code is almost the same to My ECC Service, but this time we have to break all 16 curves at the same time.
I’ll skip the challenge code.
When we look at the verify function, it is kinda obvious that we can manually set the base points.
I tried finding good base points that has well factoring order for all 16 curves. It didn’t work so well.
But while I was searching points, sage said error: u can't make the curve singular, it's dangerous.
Thankfully that’s how I got the idea for singular curve.
The curve is same for all 16 curves, $y^2 = x^3 - 3x + ?$ ($?$ is determined with the base point.) with different modulus only.
So a nice base point would make all curves singular. (2, 2) worked just fine.
Also I learned that god sage can discrete_log with even unexisting square roots in Galois Field.
sqrt(3) was needed, and it existed in none of the curves.
ex.sage
from pwn import *
from Crypto.Util.number import *
from hashlib import sha256
import os
from tqdm import tqdm
MODS = [
942340315817634793955564145941,
743407728032531787171577862237,
738544131228408810877899501401,
1259364878519558726929217176601,
1008010020840510185943345843979,
1091751292145929362278703826843,
793740294757729426365912710779,
1150777367270126864511515229247,
763179896322263629934390422709,
636578605918784948191113787037,
1026431693628541431558922383259,
1017462942498845298161486906117,
734931478529974629373494426499,
934230128883556339260430101091,
960517171253207745834255748181,
746815232752302425332893938923,
]
io = remote("my-ecc-service-2.chal.perfect.blue", 1337)
io.sendlineafter("> ", "G")
io.recvuntil("Payload: ")
recv_dat = bytes.fromhex(io.recvline().decode()[:-1])
assert len(recv_dat) == 218
original_key = recv_dat[2:10]
io.sendlineafter("> ", "V")
io.sendlineafter("Payload: ", "0202" + bytes.hex(original_key) + "00" * 13 * 16)
io.sendlineafter("> ", "G")
io.recvuntil("Payload: ")
recv_dat = bytes.fromhex(io.recvline().decode()[:-1])
assert len(recv_dat) == 218
recv_dat = recv_dat[10:]
x_ = []
for i in range(16):
x_.append(int.from_bytes(recv_dat[:13], "big"))
recv_dat = recv_dat[13:]
io.sendlineafter("> ", "V")
io.sendlineafter("Payload: ", "0000" + bytes.hex(original_key) + "00" * 13 * 16)
state = b""
chk = 0
for i in range(16):
Zp = GF(MODS[i])
gx, gy = Zp(2), Zp(2)
x = Zp(x_[i])
y1 = Zp(x^3 - 3 * x + 2).sqrt()
y2 = -y1
x -= 1
gx -= 1
sq = Zp(3).sqrt()
g_morph = (gy + sq * gx) / (gy - sq * gx)
p1_morph = (y1 + sq * x) / (y1 - sq * x)
p2_morph = (y2 + sq * x) / (y2 - sq * x)
logged1 = Integer(p1_morph.log(g_morph))
logged2 = Integer(p2_morph.log(g_morph))
logged = min(logged1, logged2)
print(logged)
assert logged < 256^10
assert len(long_to_bytes(logged)) == 10
state += long_to_bytes(logged)
assert chk == 0
new_state = b''
last = b"\x00" * 10
for i in range(16 - 1):
hsh = sha256(state + int(i).to_bytes(1, 'big')).digest()[:10]
new_state += hsh
v = int.from_bytes(hsh, 'big')
last = xor(last, hsh)
new_state += last
assert len(new_state) == 160
key = sha256(new_state).digest()[:8]
print(bytes.hex(key))
io.sendlineafter("> ", "P")
io.sendlineafter("Payload: ", "0203" + bytes.hex(key) + "00" * 13 * 16)
io.interactive()
Ironically I wasted a lot of time dealing with nonces and keys after I fully got 16 nonces. Doh!
Blocky - 4 (17 solves) & Blocky - 5 (8 solves)
(Unsolved)
It both uses square attack as I said before.
kiona provided me a nice link to study that.
https://www.davidwong.fr/blockbreakers/square_2_attack4rounds.html